At the heart of the controversy concerning quantum physics and consciousness - raised by the What the Bleep Do We Know!? movie - is a conundrum that goes by the name the measurement problem. My intention here is to introduce this problem to people not steeped in quantum physics. I will try to do this while remaining faithful to the concepts that I believe are central to the discussion at hand..
 |
| Sextans A, member of the Local Group |
One of the pervasive concepts in physics is that of a system. It is an abstraction that is used to refer to something as small as an electron orbiting the nucleus of a hydrogen atom or something as large as our own Milky Way orbiting the gravitational center of the Local Group of more than 30 galaxies. It can represent something as simple as a pair of photons, particles of light, entangled in a quantum pas de deux, or as complex as a human brain, a wet, warm, messy computational engine, sporting over 1,000 trillion synaptic connections. Even (Austrian) cats have been recruited in the service of constructing such hypothetical systems.
There is an important assumption regarding a system and that is that it can be regarded as independent or free-standing. In other words, it is meaningful to discuss a system, at least for limited purposes, as though it exisits in isolation from the rest of the world. Without this idealization the scientific enterprise as we know it would be doomed, mired in complexity. Nonetheless, we should keep in mind that it is an approximation.
 |
| A gyroscope as a demonstration of angular momentum |
Ultimately the goal of a physical theory is to offer an accurate description of the behavior of a system over a period of time. Such a description emphasizes what are considered to be significant properties, features either of the system as a whole or of its constituent parts.
Most notable among these properties of a system (or its parts) are its position and its velocity. Less concrete, but no less significant, is the property of a system which we call as its energy. Other properties include mass and electrical charge and quantities having to do with a system's rotational motion, namely its angular momentum or spin. Modern physics has added a large number of much less familiar properties to this list of quantities used to describe systems.
For our purposes, it is not so much important to know what each of these properties means individually, as it is to understand that they can be used collectively to create a "snapshot" of a system, which defines what is called its state. One can think of the state of a system as way to designate an enumeration of its properties and their corresponding values at a particular instant in time.
Measurement in General
Measurement can be seen as the process by which the properties, and hence the state, of a system are discovered. We typically imagine this as involving some sort of measuring device or apparatus, a ruler, a telescope, a radar gun, or a thermometer, for example, but in a very austere sense measurement may involve any kind and any size of physical "probe", used to determine a value for a property of a system.
Measurement in Classical Physics
In classical physics the measurement of the properties of a system, although perhaps technologically challenging, is philosophically straightforward. A measuring device can, in theory, be refined to obtain an arbitrarily precise value for a property, while at the same time inducing an arbitrarily small amount of disruption to the system as a whole.
Collectively these measured properties, drawn from a continuously-varying range of values, define the state of the system, which is, in principle, indifferent to the effect to the act of measurement.
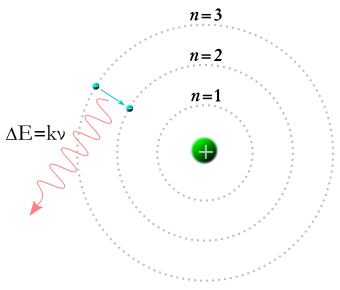 |
| Bohr atom with energy levels |
Quantum physics adds some unexpected twists to the classical theory of measurement.
For purposes of concreteness, but without loss of generality, we will use the example of a hydrogen atom consisting of a lone electron in orbit around a single proton.
It turns out that when we measure the energy of the orbiting electron we obtain not a continuous range of values, but a discrete set of values, the so-called energy levels of the system. These fixed amounts, or quanta, of energy - from which the theory derives its name - represent a departure from the classical view of the world in which quantities like energy were assumed to vary continuously
Interestingly enough, and consistent with classical theory, repeated measurements of the energy of the electron yield the very same answer. Furthermore, measurements of certain "compatible" properties, such as its angular momentum, leave the system undisrupted, and subsequent measurements of the electron's energy are unaffected.
All hell breaks out, though, when you go to measure something else.
Measurement in Quantum Physics - Second Twist
For example, if you start with a hydrogen atom in a known energy state and measure, say, the position of its electron, then the result of a subsequent measurement of its energy is no longer determined, but may take on any value from the range of allowed energy levels.
In fact the measurement of an "incompatible" property, no matter how carefully made, disrupts the system. Contrary to classical expectations, the disrupted electron is described as then occupying not one but a multiplicity of energy states, and its amount of "participation" in each of these states determines the probability that the corresponding energy level will be measured the next time around.
Troubling as this is finding may be for measurements of energy, it is even more unsettling to consider that this inevitable mixing of states also applies to measurements of position, the implication being that the electron can find itself, to a greater or lesser degree, at a multiplicity of locations!
 |
| DVD cover for Tom Stoppard's "Rosencrantz & Guildenstern" Are Dead |
Unlike measurement in classical physics which can be consigned to a secondary - and diminishing - role, measurement in quantum physics insists on playing a leading one. The choice of which properties to measure and the order in which these measurements are conducted unavoidably effect the system under observation.
It turns out that the act of measuring specific properties, most significantly energy, places a system in a stable state, referred to as a stationary state or eigenstate, in which values of those properties and compatible ones persist indefinitely. Intervening measurements of incompatible properties, though, force the system into a configuration that is a mixture of these stationary states, called a superposition. Although the outcome of individual measurements on a system described by a superposition is unpredictable, their statistical distribution is entirely determined.
 |
| A digital multimeter |
Since measurement is not a particularly important process in classical physics, it hardly commands a lot of attention. But in quantum mechanics, measurement is a first class feature of the theory and so this activity has to be much more carefully considered.
First and foremost, what does it mean to say that a measurement has occurred? Does this happen when a measuring device interacts with the system being investigated? What distinguishes these "measurement" interactions from other routine interactions between the system and its environment?
To the extent that the act of measurement is, itself, a causal chain of events described, ultimately, by quantum theory, when, if ever, can we say that it concludes? Does a measurement end, for example, when photons of light refelected off an LCD display strike the the retina of the experimenter working in her lab? What if the experimental data is collected autonomously and stored on-line? Does the measurement finally occur when the data is downloaded and viewed by the experimenter on a remote computer?
Furthermore, what is the detailed mechanism involved in transforming the quantum mechanical superposition of states into a single eigenstate state, which is characterized by the measured value of a property such as energy? How does this collapse of the wave function (an alternative name for this superposition of states), take place?
Enter Consciousness
These are some of the puzzling questions that have given rise to the variety of interpretations of quantum physics in circulation. Consciousness enters the picture because some people believe that it may be the critical feature that distinguishes measurement from other physical processes.
So consciousness is, to some extent, reasonably offered as a potential "solution" to the measurement problem of quantum mechanics. Be that as it may, it is one thing to suggest that consciousness is implicated in the collapse of the wave function, and quite another to insist it is a mechanism that allows us to project our will and desires on the physical world. This is the leap that the movie What the Bleep takes and this is why its claims are so controversial.

A Conceptual Introduction to the Measurement Problem in Quantum Physics by Marc Merlin is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
Based on a work at thoughtsarise.blogspot.com.

2 comments:
Hoping many of the participants will have read your very thoughtful comments. Well done. See you soon.
Greg McClune
Good reead
Post a Comment